OS08: Virtual Memory I

Based on Chapter 6 of [Hai19]

(Usage hints for this presentation)

Computer Structures and Operating Systems 2023
Dr. Jens Lechtenbörger (License Information)

Data Science: Machine Learning and Data Engineering (Prof. Gieseke)
Dept. of Information Systems
WWU Münster, Germany

1. Introduction

1.1. OS Plan

OS Overview (Wk 20)
OS Introduction (Wk 21)
Interrupts and I/O (Wk 21)
Threads (Wk 23)
Thread Scheduling (Wk 24)
Mutual Exclusion (MX) (Wk 25)
MX in Java (Wk 25)
MX Challenges (Wk 25)

Virtual Memory I (Wk 26)

Virtual Memory II (Wk 26)
Processes (Wk 27)
Security (Wk 28)

OS course plan, summer 2022

1.2. Today’s Core Questions

What is virtual memory?
- How can RAM be (de-) allocated flexibly under multitasking?
- How does the OS keep track for each process what data resides where in RAM?

1.3. Learning Objectives

Explain mechanisms and uses for virtual memory
- Including principle of locality and page fault handling
- Including access of data on disk
- Including shared memory
Explain and perform address translation with page tables

1.4. Previously on OS …

1.4.1. Retrieval Practice

How are processes and threads related?
What happens when an interrupt is triggered (e.g., a page fault)?

1.4.2. Recall: RAM in Hack

1.5. Big Picture

Big picture for virtual memory

The key idea of virtual memory management is to provide a layer of abstraction that hides allocation of the shared hardware resource RAM to individual processes. Thus, processes (and their threads) do not need to care or know whether or where their data structures reside in RAM.

Physical memory consists of RAM and secondary storage devices such as SSDs or HDDs. Typically, the OS uses dedicated portions of secondary storage as so-called swap areas or paging areas to enlarge physical memory beyond the size of RAM. Again, processes need neither care nor know about this fact, which is handled by OS in the background.

Each process has its own individual virtual address space, starting at address 0, consisting of equal-sized blocks called pages (e.g., 4 KiB in size each). Each of those pages may or may not be present in RAM. RAM in turn is split into frames (of the size of pages). The OS loads pages into frames and keeps track what pages of virtual address spaces are located where in physical memory.

Here you see a process with a virtual address space consisting of 10 pages (numbered 0 to 9, implying that the virtual address space has a size of 10*4 KiB = 40 KiB), while RAM consists of 8 frames (numbered 0 to 7, implying that RAM has a size of 8*4 KiB = 32 KiB). For example, page 0 is located in frame 6, while page 3 is located on disk, and frames 2, 3, and 7 are not allocated to the process under consideration.

Notice that neighboring pages in the virtual address space may be allocated in arbitrary order in physical memory. As processes and threads just use virtual addresses, they do not need to know about such details of physical memory.

Code of threads just uses virtual addresses within machine instructions, and it is the OS’s task to locate the corresponding physical addresses in RAM or to bring data from secondary storage to RAM in the first place.

1.5.1. Big Picture of VM

1.6. Different Learning Styles

The bullet point style may be particularly challenging for this presentation
You may prefer this 5-page introduction
- It provides an alternative view on
  - Topics of Introduction and Main Concepts
  - Topics of section Paging
- After working through that text, you may want to jump directly to the corresponding self-study tasks to check your understanding
  - Afterwards, come back here to look at the slides, in particular work through section Uses for Virtual Memory (not covered in the text)
Besides, Chapter 6 of [Hai19] is about virtual memory

1. Introduction
2. Main Concepts
3. Uses for Virtual Memory
4. Paging
5. Conclusions

2. Main Concepts

2.1. Modern Computers

RAM and virtual memory are byte-addressed
- 1 byte = 8 bits
- Each address selects a byte (not a word as in Hack)
  - (Machine instructions typically operate on words (= multiple bytes), though)
  - With \(n\) address bits, we address \(2^{n}\) bytes
    - E.g., 32-bit addresses for up to 2³² B = 4 GiB
Physical vs virtual addresses
- Physical: Addresses used on memory bus
  - Hack address
- Virtual: Addresses used by threads and CPU
  - Do not exist in Hack

2.2. Virtual Addresses

Additional layer of abstraction provided by OS
- Programmers do not need to worry about physical memory locations at all
- Pieces of data (and instructions) are identified by virtual addresses
  - At different points in time, the same piece of data (identified by its virtual address) may reside at different locations in RAM (identified by different physical addresses) or may not be present in RAM at all
OS keeps track of (virtual) address spaces: What (virtual address) is located where (physical address)
- Supported by hardware, memory management unit (MMU)
  - Translation of virtual into physical addresses (see next slide)

2.2.1. Memory Management Unit

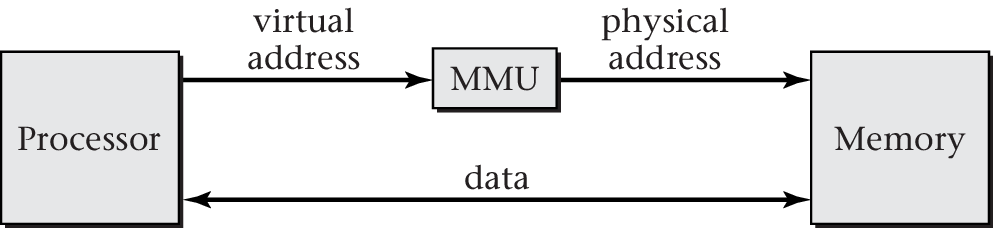
Figure 6.4 of cite:Hai17

“Figure 6.4 of [Hai17]” by Max Hailperin under CC BY-SA 3.0; converted from GitHub

2.3. Processes

OS manages running programs via processes
- More details in upcoming presentation
For now: Process ≈ group of threads that share a virtual address space
- Each process has its own address space
  - Starting at virtual address 0, mapped per process to RAM by the OS, e.g.:
    - Virtual address 0 of process P1 located at physical address 0
    - Virtual address 0 of process P2 located at physical address 16384
    - Virtual address 0 of process P3 not located in RAM at all
  - Processes may share data (with OS permission), e.g.:
    - BoundedBuffer located at RAM address 42
    - Identified by virtual address 42 in P1, maybe by 4138 in P3
- Address space of process is shared by its threads
  - E.g., for all threads of P2, virtual address 0 is associated with physical address 16384

2.4. Pages and Page Tables

Mapping between virtual and physical addresses does not happen at level of bytes
- Instead, larger blocks of memory, say 4 KiB
  - Blocks of virtual memory are called pages
  - Blocks of physical memory (RAM) are called (page) frames
  - Pages and frames share the same size (as pages are loaded into frames)

OS manages a page table per process
- One entry per page
  - In what frame is page located (if present in RAM)
  - Additional information: Is page read-only, executable, or modified (from an on-disk version)?

2.4.1. Page Fault Handler

Pages may or may not be present in RAM
- Access of virtual address whose page is in RAM is called page hit
  - (Access = CPU executes machine instruction referring to that address)
- Otherwise, page miss

Upon page miss, a page fault is triggered
- Special type of interrupt
- Page fault handler of OS responsible for disk transfers and page table updates
  - OS blocks corresponding thread and manages transfer of page to RAM
  - (Thread runnable after transfer complete)

2.5. Drawing for Page Tables

The page table

3. Uses for Virtual Memory

3.1. Private Storage

Each process has its own address space, isolated from others
- Autonomous use of virtual addresses
  - Recall: Virtual address 0 used differently in every process
- Underlying data protected from accidental and malicious modifications by other processes
  - OS allocates frames exclusively to processes (leading to disjoint portions of RAM for different processes)
  - Unless frames are explicitly shared between processes
    - Next slide

Processes may partition address space
- Read-only region holding machine instructions, called text
- Writable region(s) holding rest (data, stack, heap)

3.2. Controlled Sharing

OS may map limited portion of RAM into multiple address spaces
- Multiple page tables contain entries for the same frames then
  - Such memory areas are called shared memory
  - See smem demo later on
Shared code
- If same program runs multiple times, processes can share text
- If multiple programs use same libraries (libXYZ.so under GNU/Linux, DLLs under Windows), processes can share them

3.2.1. Copy-On-Write Drawing

Copy on write

3.2.2. Copy-On-Write (COW)

Technique to create a copy of data for second process
- Data may or may not be modified subsequently
Pages not copied initially, but marked as read-only with access by second process
- Entries in page tables of both processes point to original frames
- Fast, no data is copied
If process tries to write read-only data, MMU triggers interrupt
- Handler of OS copies corresponding frames, which then become writable
  - Copy only takes place on write
- Afterwards, write operation on (now) writable data

3.3. Flexible Memory Allocation

Allocation of RAM does not need to be contiguous
- Large portions of RAM can be allocated via individual frames
  - Which may or may not be contiguous
  - See next slide or big picture
- The virtual address space can be contiguous, though

3.3.1. Non-Contiguous Allocation

Figure 6.9 of cite:Hai17

“Figure 6.9 of [Hai17]” by Max Hailperin under CC BY-SA 3.0; converted from GitHub

3.4. Persistence

Data kept persistently in files on secondary storage
When (thread of) process opens file, file can be mapped into virtual address space
- Initially without loading data into RAM
  - See page 3 in big picture
- Page accesses in that file trigger page faults
  - Handled by OS by loading those pages into RAM
    - Marked read-only and clean
- Upon write, MMU triggers interrupt, OS makes page writable and remembers it as dirty (changed from clean)
  - Typically with MMU hardware support via dirty bit in page table
  - Dirty = to be written to secondary storage at some point in time
    - After being written, marked as clean and read-only

Typical OSs offer file systems for the persistent storage of data on disks, where persistent means that (in contrast to RAM) such data remains safely in place even if the machine is powered down. Different OSs offer different system calls for file access, and this slide focuses on a technique called memory-mapped files. Here, the file is simply mapped into the virtual address space of the process containing the thread, which invokes the system call. “Mapping” means that afterwards the file’s bytes are available starting at a virtual address returned by the system call.

Initially, no data needs to be loaded into RAM at all. If the thread now tries to access a byte belonging to the file, a page fault occurs, and the thread gets blocked. The page fault handler then triggers the transfer of the corresponding block of disk data to RAM (using metadata about the file system for address calculations). The completion of that transfer is indicated by an interrupt, in response to which the page table is updated and the corresponding page is marked as read-only and clean, where clean indicates that the page is identical to the copy stored on disk. Also, the thread accessing the file is made runnable and can access its data.

While read accesses just return the requested data, write accesses trigger another interrupt as the page is marked read-only. Now, the interrupt handler marks the page as writable and dirty. Being writable implies that further write accesses succeed without further interrupts, and being dirty indicates that the version in RAM now differs from the version on disk. Thus, when a thread requests to write data back to the file, dirty pages need to be written to disk. Afterwards, the file’s pages are marked as clean and read-only again.

3.5. Demand-Driven Program Loading

Start of program is special case of previous slide
- Map executable file into virtual memory
- Jump to first instruction
  - Page faults automatically trigger loading of necessary pages
  - No need to load entire program upon start
    - Faster than loading everything at once
    - Reduced memory requirements

3.5.1. Working Set

OS loads part of program into main memory
- Resident set: Pages currently in main memory
- At least current instruction (and required data) necessary in main memory
Principle of locality
- Memory references typically close to each other
- Few pages sufficient for some interval
Working set: Necessary pages for some interval
- Aim: Keep working set in resident set
  - Replacement policies in next presentation

As discussed so far, typically not all pages of a process are located in RAM. Those that are located in RAM comprise the resident set. For von Neumann machines at least the currently executing instruction and its required data need to be present in RAM, and demand-driven loading is a technique to provide that data on the fly.

As data is transferred in pages, one can hope that a newly loaded page does not only contain one useful instruction or one useful byte of data but lots of them. Indeed, if you think of a typical program it is reasonable to expect that the program counter is often just incremented or changed by small amounts, e.g., in case of sequential statements, loops, or local function calls. Similarly, references to data also often touch neighboring locations in short sequence, e.g., in case of arrays or objects. This reasoning is known as principle of locality, which implies that frequently only few pages in RAM are sufficient to allow prolonged progress for a thread without page faults.

Please take a moment to convince yourself that without the principle of locality caching, i.e., the transfer of some set of data from a large and slow storage area to a smaller and faster storage area, would not be effective; neither the form of caching seen here, where RAM serves as cache for disk data, nor CPU caches for RAM data.

The so-called working set (for some given time interval) of a thread T is that set of pages which allows T to execute without page faults throughout the interval. Clearly, once in a while new pages are added to the working set while other pages are removed since their contents are not necessary any longer. Note that the working set is a hypothetical construct, whose precise shape and evolution is unknown to the OS. However, the goal of memory management is to manage the resident set in such a way that is contains the working set (and ideally not much else). Page replacement policies, to be discussed in the next presentation, work towards that goal.

3.5.2. Beyond Learning Objectives: Datacenter Memory

Main memory management at Meta: [MWD+23]
- Modern memory is organized in tiers with different characteristics (e.g., cost, size, bandwidth, latency)
  - E.g.: DRAM, NVM, low-power DRAM
  - Accessible via CXL,
- Estimate page temperature as criterion for transparent page placement (TPP) in specific tier
  - Page is hot if reuse is likely within 2 minutes, warm for reuse within 10 minutes, cold otherwise
  - Idea: Move pages between faster and slower tiers based on temperature
    - Sample hardware counters (e.g., cache misses) to estimate temperature
  - Integrated into Linux kernel

4. Paging

4.1. Major Ideas

Virtual address spaces split into pages, RAM into frames
- Page is unit of transfer by OS
  - Between RAM and secondary storage (e.g., disks)
- Each virtual address can be interpreted in two ways
  1. Integer number (address as binary number, as in Hack)
  2. Hierarchical object consisting of page number and offset
    - Page number, determined by most significant bits of address
    - Offset, remaining bits of address = byte number within its page
      - (Detailed example follows)

Page tables keep track of RAM locations for pages
- If CPU uses virtual address whose page is not present in RAM, the Page fault handler takes over

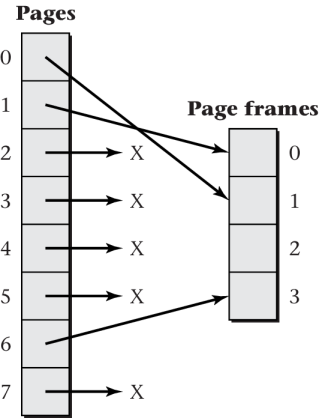
4.2. Sample Memory Allocation

Sample allocation of frames to some process
“Figure 6.10 of [Hai17]” by Max Hailperin under CC BY-SA 3.0; converted from GitHub

4.3. Page Tables

Page Table = Data structure managed by OS
- Per process: Each process has own virtual address space
Table contains one entry per page of virtual address space
- Each entry contains
  - Frame number for page in RAM (if present in RAM)
  - Control bits (not standardized, e.g., valid, read-only, dirty, executable)
    - E.g., valid bit on next slide
  - Note: Page tables do not contain page numbers as they are implicitly given by row numbers (starting from 0)

4.3.1. Sample Page Table

Consider previously shown RAM allocation (Fig. 6.10)
“Figure 6.10 of [Hai17]” by Max Hailperin under CC BY-SA 3.0; converted from GitHub
- Page table for that situation (Fig. 6.11)
  - Revisited with more and more details subsequently
    
    Valid Frame#
    
    1 1
    
    1 0
    
    0 X
    
    0 X
    
    0 X
    
    0 X
    
    1 3
    
    0 X
    - “0” as valid bit indicates that page is not present in RAM, so value under “Frame#” does not matter and is shown as “X”

Valid	Frame#
1	1
1	0
0	X
0	X
0	X
0	X
1	3
0	X

4.3.2. Use of Page Table

Translation of hierarchical address with lookup in page table

“Translation of hierarchical address with lookup in page table” by Max Lütkemeyer and Jens Lechtenbörger under CC BY-SA 4.0; from GitLab

For paging, we consider virtual addresses as hierarchical objects, where some bits enumerate pages while the remaining bits enumerate bytes within those pages. For the sake of this example, we suppose that virtual addresses have a size of 20 bits, while physical addresses only have a size of 15 bits.

It is quite common that virtual address spaces are larger than the size of physical RAM. Indeed, recall from the big picture that virtual address spaces also cover areas of secondary storage.

Moreover, recall that pages and frames have the same size. Here the size is determined by 10 bits. Thus, pages and frames share the same size of 2¹⁰ B = 1 KiB.

In practice, 4 KiB is a typical size for pages and frames, and addresses are much larger than 20 bits. (E.g., with 32 bits, we can address up to 2³² B = 4 GiB. Even “small” devices such as smartphones may have more RAM than that, requiring more address bits…)

We see that the first 10 bits making up the page number are used as index into the page table, where the frame number for the page is found. In fact, the page table shown here is the beginning of the table of the previous slide (but we omit valid bits for simplicity here).

The remaining 10 bits are used as stable offset into pages and frames as illustrated next.

4.3.3. Offset as Address Covered by Range

“Address translation with offset in covered address range” by Max Lütkemeyer and Jens Lechtenbörger under CC BY-SA 4.0; from GitLab

For a different view on the hierarchical nature of virtual addresses, let us continue the previous scenario of virtual addresses of 20 bits, to be translated to physical addresses of 15 bits, with a page size of 1 KiB.

Out of the 2¹⁰ = 1024 possible pages and 2⁵ = 32 possible frames, only the first four of each type are shown.

As before, suppose that page 0 is located in frame 1 as recorded in the page table. Thus, for translation of addresses falling into page 0, the 0 encoded in the first 10 bits of the virtual address is replaced by a 1 encoded in the first 5 bits of the physical address. Importantly, the 10 offset bits do not change under address translation.

Note how each page and each frame cover a range of addresses, starting at 0 and (given 10 bits for the offset) ending at 1023 (= 2¹⁰-1). The offset identifies a single byte in that range.

Subsequent slides provide sample calculations for address translation.

4.3.4. Address Translation Example (1/3)

Task: Translate virtual address to physical address
- Subtask: Translate bits for page number to bits for frame number
- Suppose
  - Pages and frames have a size of 1 KiB (= 1024 B)
  - 15-bit physical addresses for RAM locations, as in Hack
  - 20-bit virtual addresses, as on previous slides

First, derive following pieces of information
- Size of physical address space: 2¹⁵ B = 32 KiB
- Size of virtual address space: 2²⁰ B = 1024 KiB = 1 MiB
- 10 bits are used for offsets (as 2¹⁰ B = 1024 B)
  - Remaining 5 physical bits enumerate 2⁵ = 32 frames
  - Remaining 10 virtual bits enumerate 2¹⁰ = 1024 pages

4.3.5. Address Translation Example (2/3)

Hierarchical interpretation of addresses
- 20-bit virtual address: 10 bits for page number 10 bits for offset
- 15-bit physical address: 5 bits for frame number 10 bits for offset
Task: Translate virtual address 42
- 42 = 0000000000 0000101010
  - Page number = 0000000000 = 0
  - Offset = 0000101010 = 42
- Based on page table: Page 0 is located in frame 1
  - In general, address translation exchanges page number with frame number
    - Here, 0 with 1
- Thus, 42 is located in frame 1
  - Physical address 00001 0000101010 = 1066 (= 1024 + 42)

4.3.6. Address Translation Example (3/3)

Based on page table
- Page 6 is located in frame 3
Page 6 contains addresses between 6*1024 = 6144 and 6*1024+1023 = 7167
- Consider virtual address 7042
  - 7042 = 0000000110 1110000010
    - Page number = 0000000110 = 6
    - Offset = 1110000010 = 898
  - Replace page number 6 with frame number 3
  - 7042 is located in frame 3
    - Physical address 00011 1110000010 = 3970 (= 3*1024 + 898)

4.4. Self-Study Tasks

4.4.1. Address Translation

Answer the following questions in Learnweb.

Suppose that 32-bit virtual addresses with 4 KiB pages are used.

How many bits are necessary to number all bytes within pages?
How many pages does the address space contain? How many bits are necessary to enumerate them?
Where within a 32-bit virtual address can you “see” the page number?

4.4.2. A quiz

4.5. Challenge: Page Table Sizes

E.g., 32-bit addresses with page size of 4 KiB (2¹² B)
- Virtual address space consists of up to 2³² B = 4 GiB = 2²⁰ pages
  - Every page with entry in page table
  - If 4 bytes per entry, then 4 MiB (2²² B) per page table
    - Page table itself needs 2¹⁰ pages/frames! Per process!
- Much worse for 64-bit addresses

Outlook: Two approaches to reduce amount of RAM for page tables
1. Multilevel (or hierarchical) page tables (2 or more levels)
  - Tree-like structure, efficiently representing large unused areas
  - Root, called page directory
    - Entries cover larger address space portions
2. Inverted page tables

While the sample pages tables shown so far may seem simple to manage, pages tables can be huge in practice. As page tables are used to locate data in RAM, a naïve implementation might require the page tables themselves to be located in RAM in the first place. Let’s see how large page tables might get.

With 32-bit addresses, you see a calculation on this slide, showing that the page table for every process requires up to 4 MiB of RAM. Note that those 4 MiB are pure OS overhead, unusable for applications. So, after you booted your system half a GB of RAM may already be gone.

Although this result is already pretty bad, for 64-bit systems the situation is much worse, even if current PC processors do not use all 64 bits for addressing. Suppose 48 bits are used for virtual addresses, again with 4 KiB pages. Then 2³⁶ pages may exist per process, now maybe with 8 B per entry in the page table, leading to 2³⁹ B = 2⁹ GiB = 512 GiB. In words: A single page table might occupy 512 GiB of RAM, quite likely more than you’ve got.

Solutions to reduce the amount of RAM for page tables fall into two classes, namely multilevel page tables and inverted page tables.

The key idea of multilevel page tables is that large portions of the theoretically possible virtual address space remain unused, and such unused portions do not need to be represented in the page table. To efficiently represent smaller (used) and larger (unused) portions, the page table is represented and traversed as a tree-like structure with multiple levels. The root of that tree-like structure is always located in RAM and is called page directory. Each entry in that page directory represents a large portion of the address space, in case of 32-bit addresses and two levels (as on subsequent slides) each entry represents 1024 pages with a total size of 4 MiB. If such a 4 MiB region is not used at all, no data needs to be allocated in lower levels of the tree like structure.

The key idea of inverted page tables is that RAM is limited and typically smaller than the virtual address space. Instead of storing each allocated frame per page as discussed so far, with inverted page tables one entry exists per frame of RAM, recording what page of what process is currently located in that frame (if any). Note that only one such inverted page table needs to be maintained, whereas page tables exist per process. Also note that the number of entries of the inverted table is determined by the number of frames in RAM, instead of the (potentially much larger) number of pages of virtual address space. You will see how address translation works with inverted page tables on later slides. Right now, you may want to think about that yourself. Starting again from a page number for which the corresponding frame number is necessary, how do you locate the appropriate entry in the inverted page table? Clearly, a linear search is too slow.

5. Conclusions

5.1. Summary

Virtual memory provides abstraction over RAM and secondary storage
- Paging as fundamental mechanism
  - Isolation of processes
  - Stable virtual addresses, translated at runtime
Page tables managed by OS
- Address translation at runtime
- Hardware support via MMU with TLB
- Page table sizes pose challenges (to be revisited)

Bibliography

[Hai19] Hailperin, Operating Systems and Middleware – Supporting Controlled Interaction, revised edition 1.3.1, 2019. https://gustavus.edu/mcs/max/os-book/
[MWD+23] Maruf, Wang, Dhanotia, Weiner, Agarwal, Bhattacharya, Petersen, Chowdhury, Kanaujia & Chauhan, TPP: Transparent Page Placement for CXL-Enabled Tiered-Memory, in: Proceedings of the 28th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Volume 3, 2023. https://doi.org/10.1145/3582016.3582063

License Information

This document is part of an Open Educational Resource (OER) course on Operating Systems. Source code and source files are available on GitLab under free licenses.

No warranties are given. The license may not give you all of the permissions necessary for your intended use.

In particular, trademark rights are not licensed under this license. Thus, rights concerning third party logos (e.g., on the title slide) and other (trade-) marks (e.g., “Creative Commons” itself) remain with their respective holders.