Combinational Circuits I

(Usage hints for this presentation)

IT Systems, Summer Term 2025
Dr. Jens Lechtenbörger (License Information)

Chair of Machine Learning and Data Engineering (Prof. Gieseke)
Dept. of Information Systems
University of Münster, Germany

1. Introduction

1.1. Today’s Core Question

How can we perform arithmetic and logic operations on integer numbers, starting from Boolean logic?
- Based on Chapter 2 of (Nisan and Schocken 2005)

1.2. Learning Objectives

Compute 2’s complement of a binary number and use it for addition and subtraction
Build, test, and analyze combinational circuits leading to the Hack ALU (Project 2)
- Half and full adder, Ripple-Carry Adder (Add16)
- Incrementer (Inc16)
- ALU
Determine ALU operation based on control bits

1.3. Retrieval Practice

Prior knowledge
- How do you add two numbers with pen and paper, say 4242 + 6789?
Please take a brief break and add two decimal numbers here. Quite likely, in elementary school you learned how to do so with pen and paper, writing the numbers underneath each other and adding them digit by digit.
- What is 101010 in decimal?
Convert the shown binary number to decimal.

What is a multi-bit chip?

Agenda

Part 1
Break for self-study
Part 2

2. Addition

2.1. Pen-and-paper method

We add digits from right to left, possibly with “carry”

In decimal

          4242
       +  6789
Carry:   11110
         -----
         11031

In binary

          10110111
       +  11000101
Carry:   100000110
         ---------
         101111100

Note
- Rightmost (lowest) position with carry 0
  - Only need to add 2 bits
- Other positions need to add 3 bits
For the rightmost position, we just need to add two digits, while other positions may have a nonzero carry. Such a carry needs to be added as third digit.
- Both sample results are 1 digit larger than the inputs
  - Overflow in case of fixed digits/bits; incorrect result if discarded
  The result of an addition might need more digits than its inputs. If we use a fixed number of digits, the result might be too large to be represented. Then, an overflow occurs, and the result is incorrect. We expand on that thought next.

2.2. Adding with fixed bits

Binary addition of previous slide
- 10110111 + 11000101 = 101111100 (= 380)
- Suppose restriction to 8 bits
  - Largest number is \(2^{8} - 1 = 255\)
  - 8-bit-result (drop leading 1 and 0): 1111100 (= 124)
    - Incorrect, overflow, bug
    - Examples at Wikipedia

Insight (recall Fail task)
- Restricting to \(n\) bits corresponds to Modulo operation
  - \(\mod 2^n\)
- \(n=8\): 10110111 + 11000101 = 1111100 mod 256

3. 2’s Complement

3.1. Definitions

Consider \(n\)-bit number \(k\)
- \(k_c = 2^n - k\) is 2’s complement of \(k\) (and vice versa)
  
  Given an \(n\)-bit number \(k\), we say that \(2^n\) - \(k\) is the 2’s complement of \(k\).
  - Note: \(k + k_c = 2^n = 0 \mod 2^n\), i.e., complementary numbers add up to zero
  - E.g., \(n=4\), \(2^4 = 16\): \(1\) and \(15\) are complements of each other; \(8\) is complement of itself
  In other words, 2’s complement defines \(n\)-bit numbers to be complements of each other if their sum is \(2^n\).
  
  Again in other words, their sum is 0 modulo \(2^n\).
  
  E.g., with 4 bits, 1 and 15 are complements of each other as they add up to 16.
- If most significant bit of \(k\) is 0, interpret as (usual) positive number
- If most significant bit is 1, interpret bit pattern as negative number: \(k = -k_c\)
  - E.g., \(15 = (1111)_2\) and \(8 = (1000)_2\) are interpreted as negative numbers under 2’s complement: \((1111)_2 = -1\) and \((1000)_2 = -8\)
  Recall that the leading bit of a number is the most significant one. If the most significant bit of a number is 0, we interpret the bit pattern as ordinary, positive binary number.
  
  If the most significant bit of a number is 1, we interpret the bit pattern as negative number under 2’s complement. Namely, we interpret such a bit pattern as negative of its complement. This interpretation makes sense as both numbers (in the usual interpretation) add up to 0 as remarked above.
  
  You see examples here.

3.2. Example and Conversion

\(2^n\) signed numbers between \(-2^{n-1}\) and \(2^{n-1} - 1\)

Under this interpretation, with \(n\) bits we represent \(2^n\) signed numbers in the range shown here.
- E.g., \(n=4\)
```
0   0000
1   0001    1111   -1
2   0010    1110   -2
3   0011    1101   -3
4   0100    1100   -4
5   0101    1011   -5
6   0110    1010   -6
7   0111    1001   -7
            1000   -8
```
E.g., with 4 bits under 2’s complement, these numbers arise.
- Note
  - Positive numbers start with 0
    - Usual binary number
  - Negative numbers start with 1
  - To convert a number
    - Leave all trailing 0’s and first 1 intact, flip all remaining bits or
    - Flip all bits and add 1
Thus, positive numbers start with 0 and are our usual binary numbers. In contrast, negative numbers start with 1. To convert a number, two methods are shown here.

Maybe the second method is easier to remember: Flip all bits and add 1. Please try this out on your own.

3.3. Addition with 2’s Complement

We just add bit patterns, mod \(2^n\)
- No need to treat negative numbers specially
- Subtraction as addition with 2’s complement
  - Example
```
2-5 = 2 + (-5):  0010
               + 1011
                 ----
                 1101 = -3
```
- In Hack, overflows will be ignored
  - Programming bug

4. Building an Adder Chip

Sequence of chips
- Increasing complexity
  1. HalfAdder: Adds two bits, produces two output bits
  2. FullAdder: Adds three bits, produces two output bits
  3. Add16: Adds two 16-bit numbers, produces 16-bit output

4.1. Half Adder

a	b	carry	sum
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Half Adder

Figure under CC0 1.0

Several implementations possible
- DNF with Not, And, Or
- Alternative based on two gates
  - sum = Xor(a, b)
  - carry = And(a, b)

4.2. Full Adder Specification

a	b	c	carry	sum
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Full Adder

Figure under CC0 1.0

Several implementations possible
- DNF with Not, And, Or
- Based on two Half Adders, see next slide

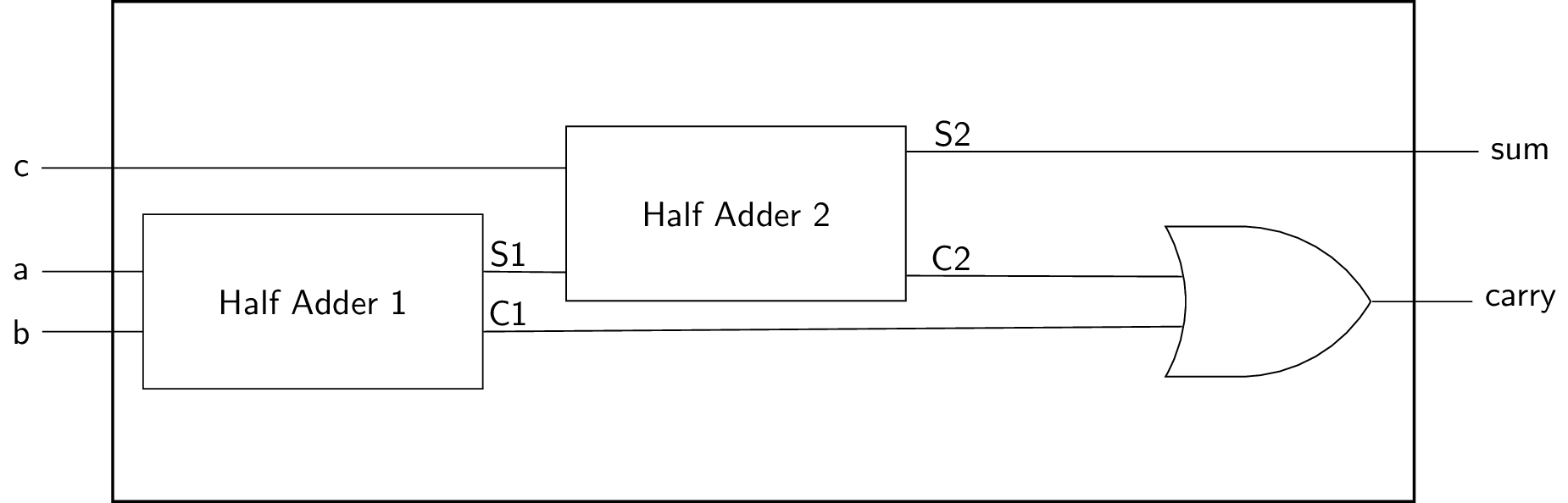
4.3. Full Adder Implementation

Full Adder based on Half Adders

Figure under CC0 1.0

Internal names
- C1 = And(a, b)
- S1 = Xor(a, b)
- C2 = And(S1, c) = And(Xor(a, b), c)
- S2 = Xor(S1, c) = Xor(Xor(a, b), c)
Outputs: carry = Or(C1, C2); sum = S2

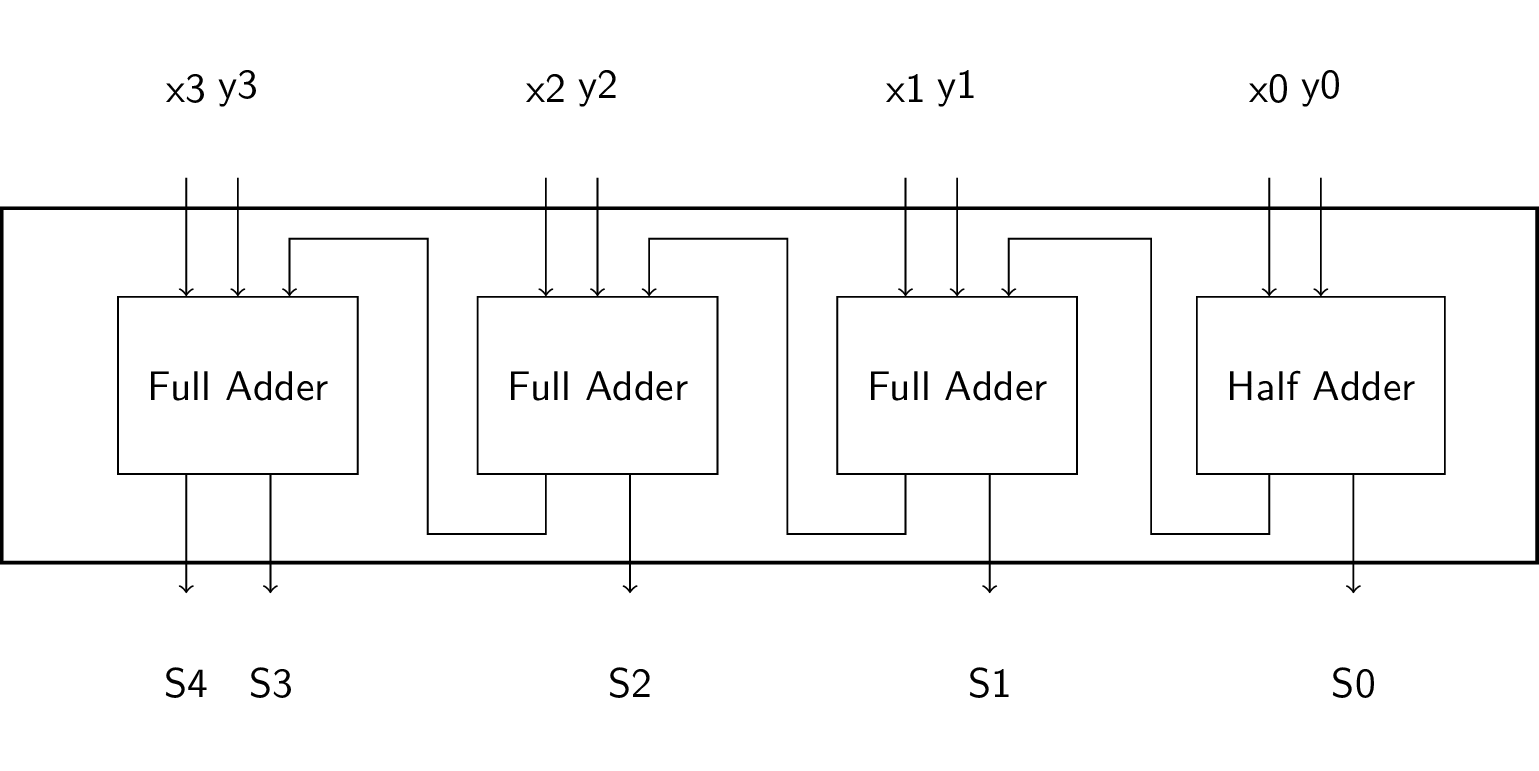
4.4. Ripple-Carry 4-bit Adder

Ripple-Carry 4-Bit Adder

Figure under CC0 1.0

Add 4-bit numbers \(x=x_3 x_2 x_1 x_0\) and \(y=y_3 y_2 y_1 y_0\)
- Produce 5-bit number \(S=x+y = S_4 S_3 S_2 S_1 S_0\)

By chaining 1-bit adders one after the other, we can build adders for any number of bits. Here you see an example for a 4-bit adder. As observed earlier, the rightmost adder can be a half adder as only two digits need to be added without carry.

The construction here is called ripple-carry adder as the carry bit may propagate, or ripple, from the right all the way to the left. This causes some propagation delay before the computation is completed, and several adder optimizations exist to speed up the process.

However, such optimizations are beyond our topics.

Regarding the number and naming of outputs, there is some freedom. The adder shown here produces 5 output bits, of which the final one can also be understood as carry bit. Alternatively, the fifth bit may be omitted entirely, to produce again a 4-bit number. As observed previously, with less than 5 output bits, overflows may occur, which lead to incorrect results.

Note that the adder works independently of any assumption regarding the interpretation of resulting bits. The adder can be understood to add positive numbers (without overflows), or we may interpret inputs and output as numbers under 2’s complement (which requires to ignore the fifth bit).

In class, we may build a ripple-carry adder for 16-bit addition. That adder has two 16-bit inputs and produces one 16-bit output, all of which are interpreted as numbers under 2’s complement (potentially leading to overflows).

5. Self-Study Tasks

5.1. Negative Numbers

What is -42 as 7-bit number in 2’s complement?

5.2. Recall Adders

What parts make up a half adder? A full adder? A ripple-carry adder?

Bibliography

Nisan, Noam, and Shimon Schocken. 2005. The Elements of Computing Systems: Building a Modern Computer from First Principles. The MIT Press. https://www.nand2tetris.org/.

License Information

Source files are available on GitLab (check out embedded submodules) under free licenses. Icons of custom controls are by @fontawesome, released under CC BY 4.0.