Boolean Logic II

(Usage hints for this presentation)

IT Systems, Summer Term 2026
Dr.-Ing. Matthes Elstermann

(Author and License Information)

1. Introduction

Part 1
- Introduction
- Boolean Logic
Break for self-study
Part 2

2. Boolean Circuits

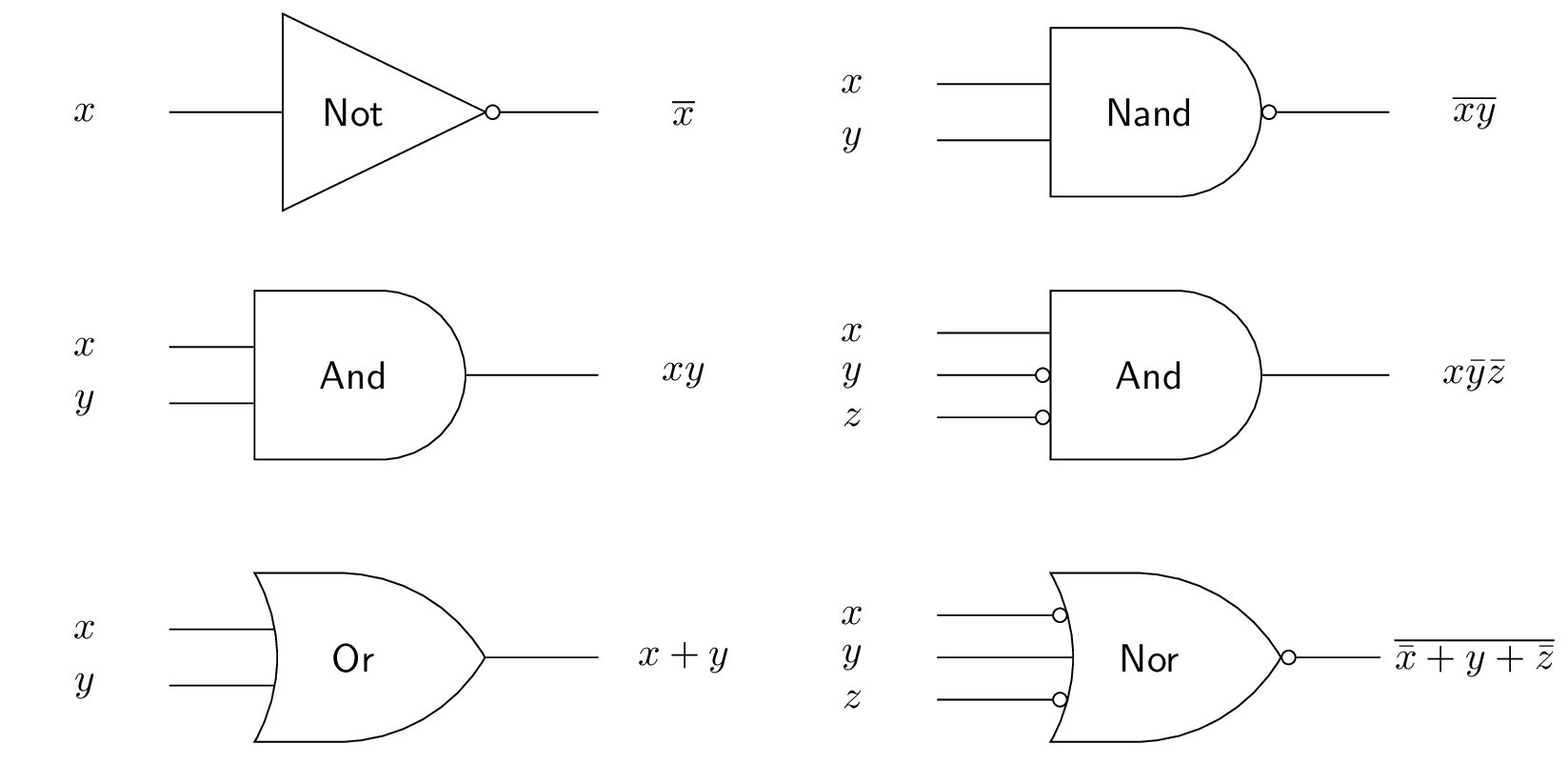
2.1. Symbols for Logical Gates

Symbols for logical gates

“Symbols for logical gates” under CC0 1.0; from GitLab

2.2. Fan-In and Circuits

Gate’s interface defines number of inputs
- Gates and chips have pins for inputs and outputs
- Number of inputs called fan-in
  
  The interface of a logical gate defines how many inputs it accepts and how many outputs it produces. In fact, in hardware, the inputs and outputs may be visible as pins, which can be wired to other gates or chips to form larger circuits.
  
  The number of inputs for a gate is called its fan-in.
- Fan-in is 2 for Nand, And, Or in case of Nand2Tetris
  - With associative and commutative operations, gates of any fan-in work in any order of computation
    
    For typical operations such as Nand and Or, the fan-in is 2 in Nand2Tetris.
    
    If you think about it, we might also build gates with a larger fan-in.
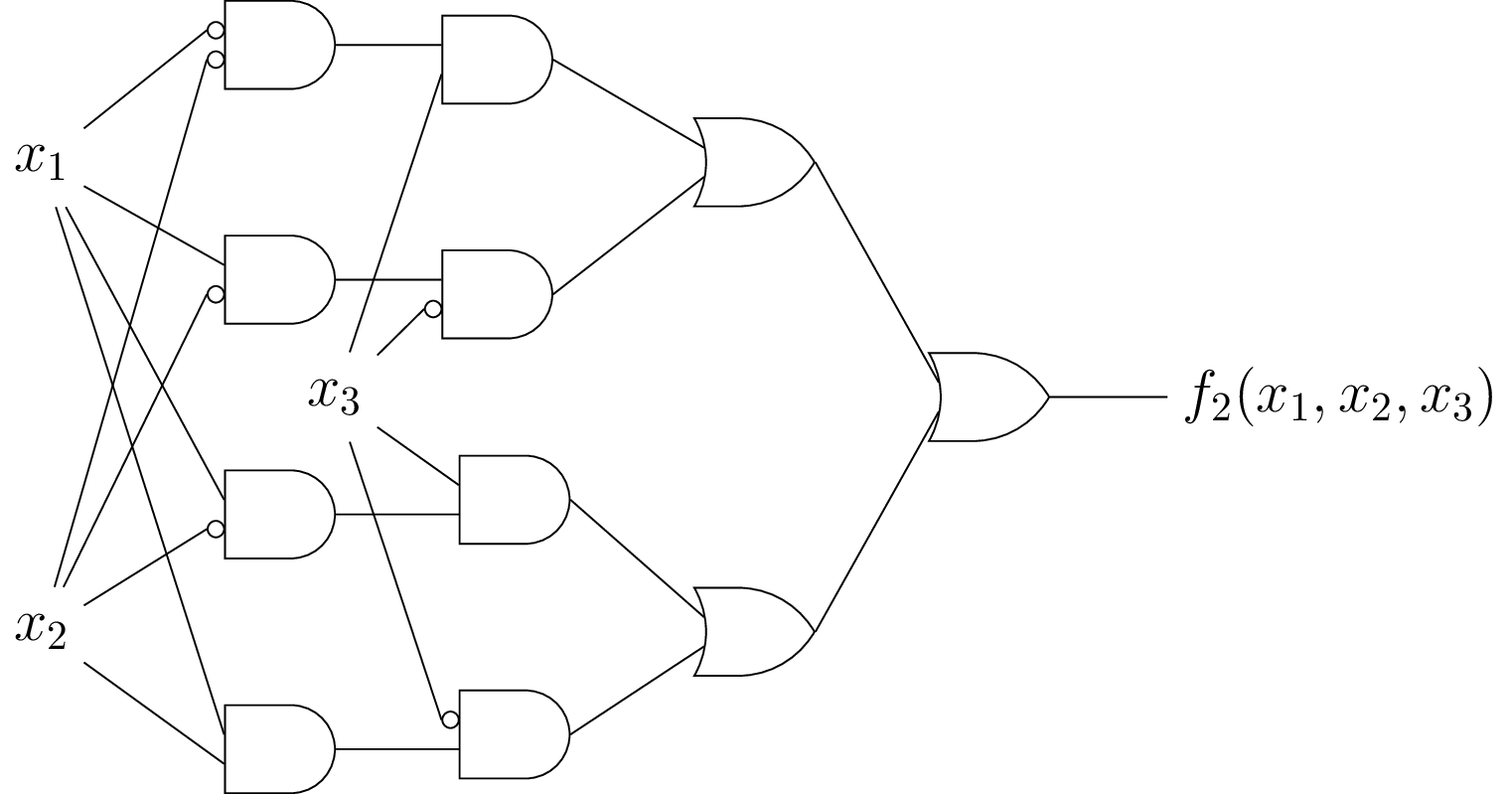
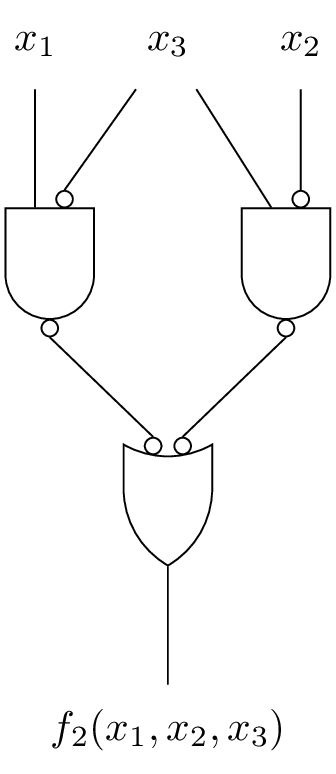
  - Consider
    
    \begin{eqnarray*} &&f_2(x_1, x_2, x_3) = \\ && \bar{x_1}\bar{x_2}x_3 + x_1\bar{x_2}\bar{x_3} + x_1\bar{x_2}x_3 + x_1 x_2 \bar{x_3} \end{eqnarray*}
    
    \(x_1\) \(x_2\) \(x_3\) \(f_2(x_1, x_2, x_3)\)
    
    0 0 0 0
    
    0 0 1 1
    
    0 1 0 0
    
    0 1 1 0
    
    1 0 0 1
    
    1 0 1 1
    
    1 1 0 1
    
    1 1 1 0
    
    Consider the function \(f_2\) shown here. If we want to implement \(f_2\) as circuit starting from the DNF, the fan-in defines how many gates we need.

\(x_1\)	\(x_2\)	\(x_3\)	\(f_2(x_1, x_2, x_3)\)
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

Alternatives
- Fan-in of 2
  Figure under CC0 1.0
- Fan-in of 4
  Figure under CC0 1.0

2.3. Multi-Bit and Multi-Way Gates

Multi-bit gates/chips: Inputs are n-bit operands each
- E.g., And16: And for 16-bit numbers is applied bit-by-bit
  - And16(1100110011001100, 00001111000011110000) = 0000110000001100
  - Use 16 And gates in implementation

Multi-way gates/chips: More than 2 inputs, i.e., fan-in larger than 2
- E.g., Or8Way: 8 inputs; out = 1 if at least one of them is 1
  - Use suitable number of Or gates in implementation

3. Sample Transformations

3.1. Sample Algebraic Simplifications

Simplify \(f_2(x_1, x_2, x_3)\)

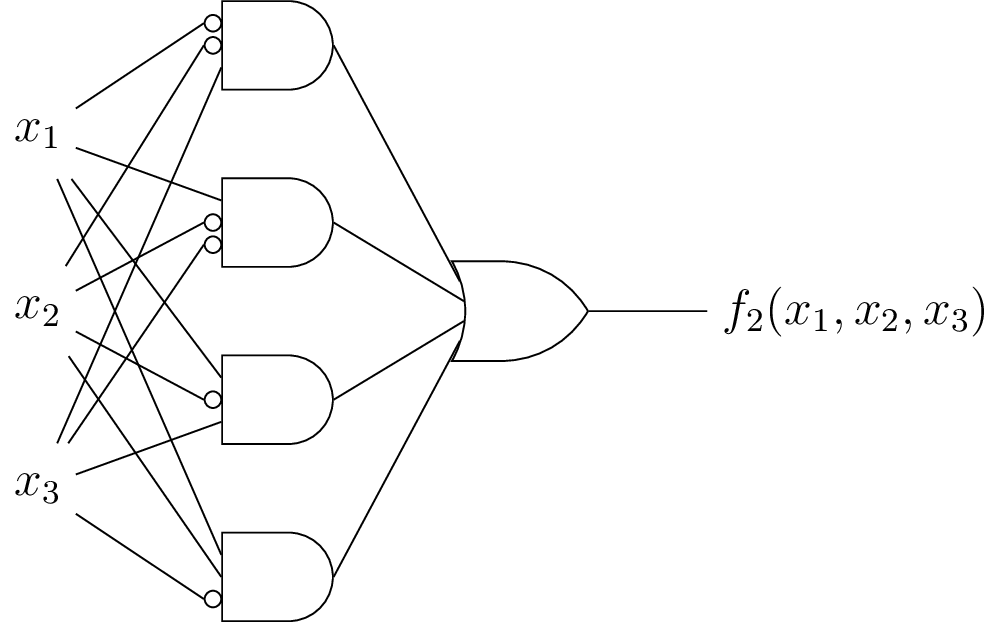
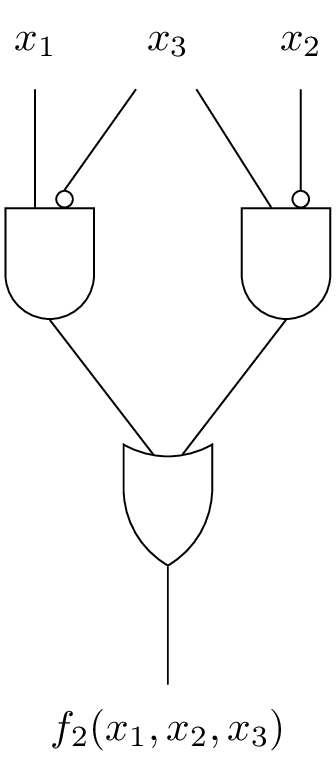
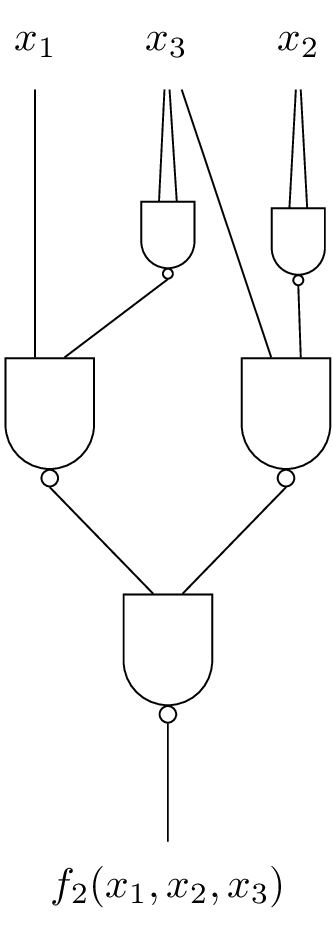
\begin{eqnarray*} &&= \color{darkred}{\bar{x_1}\bar{x_2}x_3} + \color{darkblue}{x_1\bar{x_2}\bar{x_3}} + \color{darkred}{x_1\bar{x_2}x_3} + \color{darkblue}{x_1 x_2 \bar{x_3}}\\ &&= \color{darkred}{(\bar{x_1} + x_1)\bar{x_2}x_3} + \color{darkblue}{(\bar{x_2} + x_2)x_1\bar{x_3}}\\ &&= \color{darkred}{\bar{x_2}x_3} + \color{darkblue}{x_1\bar{x_3}} \end{eqnarray*}

Simplify \(\bar{x_1}\bar{x_2}x_3 + x_1\bar{x_2}x_3 + x_1 x_2 x_3\)

Please try to proceed similarly here.
- \(\color{darkred}{\bar{x_1}\bar{x_2}x_3} + \color{darkred}{x_1\bar{x_2}x_3} + \color{darkblue}{x_1\bar{x_2}x_3} + \color{darkblue}{x_1 x_2 x_3}\)
- \(\color{darkred}{(\bar{x_1} + x_1)\bar{x_2}x_3} + \color{darkblue}{(\bar{x_2} + x_2)x_1x_3}\)
  
  Here, we first duplicate the second minterm, which is allowed as x equals x + x. Afterwards, we can use each of the duplicates for a separate application of distributivity.

3.2. DNF to All-Nand, Graphically

Sample SOP circuit for All-Nand

Figure under CC0 1.0

Sample SOP circuit for All-Nand with Negations

Figure under CC0 1.0

Sample SOP circuit transformed to All-Nand

Figure under CC0 1.0

4. Multiplexors and De-Multiplexors, Project 1

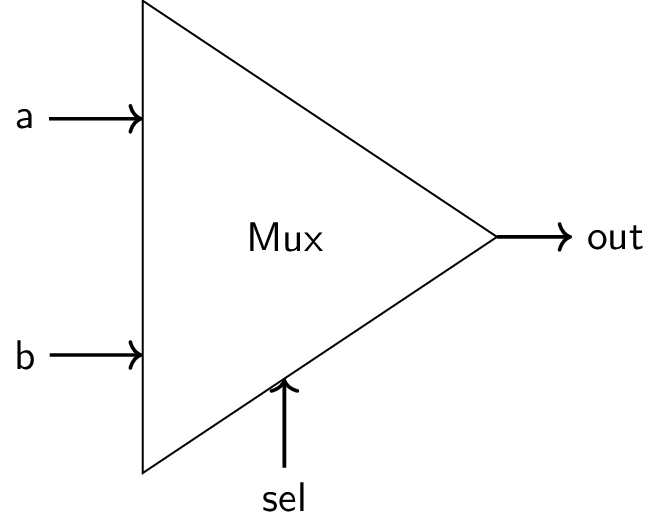
4.1. Mux

Truth table

a b sel out

0 0 0 0

0 0 1 0

0 1 0 0

0 1 1 1

1 0 0 1

1 0 1 0

1 1 0 1

1 1 1 1

a	b	sel	out
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

Specification (from Mux.hdl)
- If sel==1 then out=b else out=a.
  
  Figure under CC0 1.0
  
  A multiplexor, or mux for short, implements the if statement shown here. Based on a selector bit, it forwards one of two inputs to its single output.
- Alternative view on truth table
  
  sel out
  
  0 a
  
  1 b

sel	out
0	a
1	b

Self-study
- Implement Mux
  - Start from truth table, simplify (task in Learnweb)
  - Use Not, And, Or gates
Maybe in class
- Implement Mux8Way16

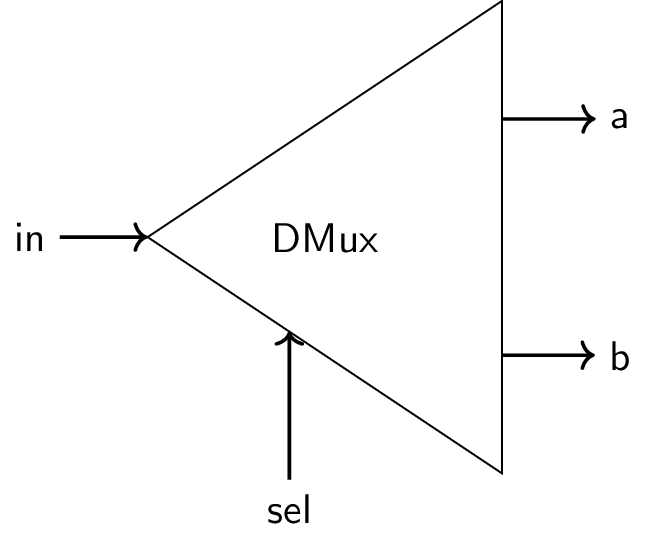
4.2. DMux

Truth table

in sel a b

0 0 0 0

0 1 0 0

1 0 1 0

1 1 0 1

in	sel	a	b
0	0	0	0
0	1	0	0
1	0	1	0
1	1	0	1

Specification (from DMux.hdl)

{a,b} = {in,0} if sel==0
        {0,in} if sel==1

De-Multiplexor

Figure under CC0 1.0

Self-study
- Implement DMux
  - Read from truth table
  - Use one Not, two And gates
Maybe in class
- Implement DMux8Way

4.3. Project 1

Given: Nand(a,b), false

a b Nand(a, b)

0 0 1

0 1 1

1 0 1

1 1 0
Build:
- Not(a) = …
- true = …
- And(a,b) = …
- Or(a,b) = …
- Mux(a,b,sel) = …
- Etc. - 12 gates altogether
See Chapter 1 of (Nisan and Schocken 2005)

a	b	Nand(a, b)
0	0	1
0	1	1
1	0	1
1	1	0

5. Conclusions

5.1. Summary

Boolean logic is formal foundation for functionalities of gates and chips
DNF provides canonical representation for Boolean functions
- Can be read off truth table
- Simplification with laws
Project 1 builds on Boolean logic to construct gates and circuits
- Starting from {Nand}, which is functionally complete

5.2. Q&A

Please ask questions and provide feedback on a regular basis
- Something confusing?
  - What did you understand? Where did you get lost?
- Maybe suggest improvements on GitLab
  - Did you create exercises, experiments, explanations?
- Use Learnweb: Shared, anonymous pad and MoodleOverflow

Bibliography

Nisan, Noam, and Shimon Schocken. 2005. The Elements of Computing Systems: Building a Modern Computer from First Principles. The MIT Press. https://www.nand2tetris.org/.

License Information

Source files are available on GitLab (check out embedded submodules) under free licenses. Icons of custom controls are by @fontawesome, released under CC BY 4.0.